DEFINICIÓN:
El complemento de un conjunto A es el conjunto de elementos que no
pertenecen a A, es decir, la diferencia del conjunto universal U y del A. se
denota el complemento de A por A'
Notación:
El conjunto complemento se denota por una
barra horizontal o por el superíndice <<C>> por lo que se tiene
A=C. Y también C=A
U=CONJUNTO UNIVERSO
A=CONJUNTO
Aº= El complementario de A
es otro conjunto A cuyos elementos son todos
aquellos que no están en A:
cuyos elementos son todos
aquellos que no están en A:
(Luna, 2014)
PROPIEDADES
Conjuntos
U= {3, 4, 5, 6,8}
A= {4, 5,6,}
El conjunto universal contiene todos los elementos en consideración, y
el conjunto vacío no
contiene a ninguno, se tiene lo siguiente:
El universo no tiene complemento por lo tanto nos queda
conjunto vacío.
El conjunto vacío no tiene elementos por lo tanto el
complemento es el conjunto universo.
Propiedad involutiva: El complementario del complementario de A es el propio A:
(A∁)∁ = A
La unión: de un conjunto y su
complementario es el conjunto universal: A ∪ A∁
= U
La disyunción:
de un conjunto y su complementario son disjuntos: A ∩ A∁ = ∅
Propiedad transitiva:
El
complementario de A está contenido en
el complementario de cualquier subconjunto de A: B ⊆ A implica que A∁ ⊆ B∁
(Seymaour,
1991)


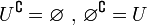



No hay comentarios:
Publicar un comentario